TASK 3

Question 1

1 - To store the elements of the set in an unordered fashion but will take longer time because these operation require a large amount of searching for elements.

2 – Method for storing elements using an arbitrary ordering of elements of the universal set. This method makes computing combination of set easy.

Example 1 : Let U = { 1,2,3,4,5,6,7,8,9,10} and element of U is in increasing order, that is ai = i

1) What bit strings that represents the subset of odd integer in U?

= the set of odd integer in U is {1,3,5,7,9}

1 0 1 0 1 0 1 0 1 0

1 2 3 4 5 6 7 8 9 10

= 10 1010 1010

2) What bit strings that represents the subset of even integer in U?

= the set of even integer in U is {2,4,6,8,10}

0 1 0 1 0 1 0 1 0 1

1 2 3 4 5 6 7 8 9 10

= 01 0101 0101

3) What bit strings that represents the subset of integer not exceeding 5 in U?

= the set of integer not exceeding 5 in U is {1,2,3,4,5}

1 1 1 1 1 0 0 0 0 0

1 2 3 4 5 6 7 8 9 10

COMPLEMENT

Example 2 :

 From example 1, we have seen that the bit string for the set {1,3,5,7,9} with U={1,2,3,4,5,6,7,8,9,10} is 1010101010

the bit string for the complement of this set is by replacing Os and 1s and vice versa.

from 10 1010 1010 ------------------------> 01 0101 0101

INTERSECTION

Intersection occurs when sets are compared to find the common elements between them. Given the Universal set has {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, and Set A = {1, 2, 3, 4, 5} and Set B = {1, 3, 5, 7, 9}
Bit representation for set A is 1111100000, 

Bit representation of set B is 1010101010.

For A  ∩ B

1111100000
1010101010

1010100000

UNION

Union occurs when sets are combined to add up all the elements of member set.

For A ∪ B,

1111100000
1010101010

1111101010

Question 2

Binary Relation

Definition: A binary relation between two sets X and Y is a subset       means that it is a set of ordered pair (x,y) ∈ X x Y.

Reflexive: A relation R on a set N is reflexive if n ∈ N, then (n,n) ∈ R [ meaning (v,v) belongs to R.] So for all x in X it holds that xRx. Take for example the set of numbers {3, 5, 6, and 10}. The relation of “less than or equals to” on the set is reflexive because every numbers can be mapped back to itself, so the members of this relation are {(3,3) , (3,5) , (3,6) , (3,10) , (5,5) , (5,6) , (5,10) ,  (6,6)  , (6,10) , (10,10)}

Symmetric: A relation R on a set N is symmetric if and only if (a,b) ∈ R and (b,a) ∈ R. So for all x and y in X it holds that if xRy then yRx. For example, 
for the equation a+b =9,
if a = 4, and b = 5,

or a = 5, and b = 4,
a+b will still be 9 regardless of the values of a and b.

Asymmetric: A relation R on a set N is asymmetric 
If (a,b) ∈ R but (b,a) ∈ R then a = b.
If (a,b) ∈ R but (b,a) ∈ R = p,
then "a = b" = q,
the truth table for this relation will be 
 

p	q	p → q
T	T	T
T	F	F
F	T	T
F	F	T

Transitive: A relation R on a set N is transitive if whenever (a,b) ∈ R and (b,c) ∈ R, then we can deduce that (a,c) ∈ R. Let's say that is a > b, and b > c, then we can deduce that a > c.

FUNCTION

Definition of function: Function is a relationship between two quantities,one of each is completely determined by the value of each other.


BOOLEAN FUNCTION

Consider a Boolean algebra of subsets   generated by a set  , which is the set of subsets of   that can be obtained by means of a finite number of the set operations union, intersection, and complementation. Each Boolean function has a unique representation (up to order) as a union of complete product

Types of function

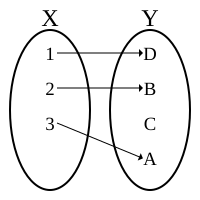
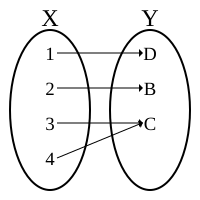
1) INJECTIVE ( one to one function )

Only one element of domain is mapped to any given one

element of the range.

2) SURJECTIVE 

Function maps onto group set A onto the entirely of the set B,not just over a piece of it

3) BIJECTIVE

A function f from A to B is called onto, or a surjection, if and only if for every element b ∈ B there is an element a ∈ A with f (a) = b.

4) INVERSE FUNCTION

Let f be a one-to-one correspondence from the set A to the set B. The inverse function of f is the function that assigns to an element b belonging to B the unique element.Hence,f-1(b)=a when f(a) = b.

     5) COMPOSITE FUNCTION

Definition :

Composite function is formed by plugging in an equation into variables of another equation in stead of random variables.

Besides, we can states (f ◦ g)(a) as f [g(a)].

 f [g(x)] is generally not equal to g [f(x)]

Example 1:

Give function  f (x) = 2x + 3 and g(x) = 3x + 2.

Find (f ◦ g)(x) and the value of (f ◦ g)(5).

(f ◦ g)(x) = f (g(x))

       =f (3x + 2)

               =2(3x + 2) + 3

               = 6x + 7

(f ◦ g)(5) =6(5) + 7

               =37

Therefore, (f ◦ g)(5) = 37

Example 2:

Give function  f (a) = 4a + 5 and g(a) = 3a + 2.

Find (g◦ f)(a) and the value of (f ◦ g)(2).

 (g ◦ f )(a) = g(f (a))

               = g(4a + 5)

               = 3(4a + 5) + 2

               = 12a + 15 + 2

               = 12a + 17

(f ◦ g)(2) = 12(2) + 17

              =24 + 17

              =41

Therefore, (f ◦ g)(2) = 41