Task 7

Multiplication Principle

Definition of Multiplication Principle

·         Multiplication Principle states: If an event occurs in m ways and another event occurs independently in n ways, then the two events can occur in m × n ways.

Solved Example on Multiplication Principle

Ali can choose 6 types of ice cream for his desserts while Alex can choose 6 different types of chocolate as his desserts. So how many possible outcomes is there for their choices?
The answer is 6 (choice that can be made by Ali) X 6 ( other choices that can be made by Alex ) = 36. There are 6 different chocolates that Alex can choose from for every one of 6 ice creams that Ali can choose to form the combination. So there is 36 combinations for this situation.

Addition Principle

Definition of Addition Principle

·         Addition Principle states: If an event can occurs in m ways and n ways, then the one events can occur in m + n ways.

Solved Example on Multiplication Principle

Ali can now choose his one dessert from 6 flavours of ice creams and 6 types of chocolates as his dessert.  How many possible outcome is there for this situation?
The answer is 6 (types of ice cream) + 6 (types of chocolates) = 12. Ali can choose as he wills from 12 desserts made up from 6 ice creams and 6 chocolates.

Combination Principle

Definition of Combination Principle

·         A combination of both Addition Principle and Multiplication Principle?

Solved Example on Multiplication Principle

Ali wants to have his lunch in a food court. He wants to have only 1 or 2 meals from the vast variety of dishes served in the food court. He can choose from 5 Chinese cuisines, 6 Malay cuisines, and 8 types of desserts. So what choices does he have?

If he only wishes to have 1 meal, he can choose from 5 (Chinese cuisines) + 6 ( Malay cuisine) + 8 (desserts) =  19 choices.

If he wishes to have 2 meals of different cuisine, he can choose from 19 X 18 = 342 combinations of meals.
So, if he wishes to have only 1 or 2 meals from the food court, there is 342 + 19 = 361 ways he can have his lunch in the food court.

Permutation

Definition: A way, esp. one of several possible variations, in which a set or number of things can be ordered or arranged especially in linear order.

Formula: _n P _r = n! / (n-r)! 

Problem Solving

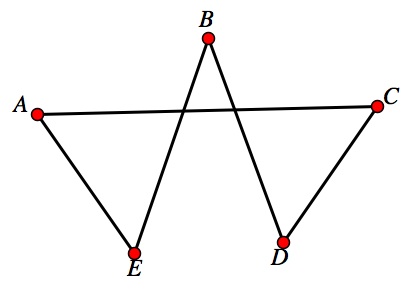
When A,B,C, D and E are lined up for photo shooting sessions, but there’s only 3 persons are allowed. How many different positions can they create for the session?

The answer is 5 X 4 X 3 which is 60 ways.

Or

120 (5!)  / 2 (2!) = 60.
Which means we can choose 5 person from the start. Then we select another one from the leftover 4. At last we select the last person from the leftover 3.

Combination

Definition: A way of selecting several things out of a larger group, where (unlike permutations) order does not matter.

Formula: _nC_r = _nP_r / r! (n-r)! 

Problem Solving

When A,B,C, D and E are lined up for photo shooting sessions, but there’s only 3 persons are allowed. But then the position doesn’t matters.

The answer is 60 (_nP_r    ) / 3! (r!) X 2! (n-r)! = 5.

task 6

QUESTION 1: (DEFINITION)

EULER PATH

An Euler path is a path that uses every edge of a graph 

exactly once

An Eulerian trail (or Eulerian path) is a trail in a graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycleis an Eulerian trail which starts and ends on the same vertex. 

Euler proved that a necessary condition for the existence of Eulerian circuits is that all vertices in the graph have an even degree, and stated without proof that connected graphs with all vertices of even degree have an Eulerian circuit.


EULER CIRCUIT

An Euler circuit is a circuit that uses every edge of a graph 

exactly once.

Every vertex of this graph has an even degree, therefore this is an Eulerian graph.

 Following the edges in alphabetical order gives an Eulerian circuit/cycle.

QUESTION 2.
HOW TO DIFFERENTIATE BETWEEN EULER PATH AND EULER CIRCUIT?

ANSWER:

Euler Path	Euler Circuit
A path that uses every edges of a graph exactly once	A circuit that uses every edges of a graph exactly once
Start and end at different vertices	Start and end at same vertex
If a graph has Euler path, then it must have exactly 2 odd vertices	If a graph has Euler circuit, then all of its vertices must be even vertices

HAMILTON PATH

In the mathematical field of graph theory, a Hamiltonian path (or traceable path) is a path in an undirected graph that visits each vertex exactly once. A Hamiltonian Path can start from one point and ends up at another point.




 HAMILTON CYCLE

A Hamiltonian cycle (or Hamiltonian circuit) is a Hamiltonian path that is a cycle. Hamiltonian Cycle starts from one point and returns to the starting point after traveling it's path.














QUESTION 5
HOW TO DIFFERENTIATE BETWEEN HAMILTON PATH AND HAMILTON CIRCUIT?

ANSWER:

Hamilton Path	Hamilton Circuit
A path that passed every vertex exactly once	A simple circuit that passed every vertex and return to the starting vertex
There is a vertex that has one degree	There is a 2 or more than one degree in the vertex