Task 7

Multiplication Principle

Definition of Multiplication Principle

·         Multiplication Principle states: If an event occurs in m ways and another event occurs independently in n ways, then the two events can occur in m × n ways.

Solved Example on Multiplication Principle

Ali can choose 6 types of ice cream for his desserts while Alex can choose 6 different types of chocolate as his desserts. So how many possible outcomes is there for their choices?
The answer is 6 (choice that can be made by Ali) X 6 ( other choices that can be made by Alex ) = 36. There are 6 different chocolates that Alex can choose from for every one of 6 ice creams that Ali can choose to form the combination. So there is 36 combinations for this situation.

Addition Principle

Definition of Addition Principle

·         Addition Principle states: If an event can occurs in m ways and n ways, then the one events can occur in m + n ways.

Solved Example on Multiplication Principle

Ali can now choose his one dessert from 6 flavours of ice creams and 6 types of chocolates as his dessert.  How many possible outcome is there for this situation?
The answer is 6 (types of ice cream) + 6 (types of chocolates) = 12. Ali can choose as he wills from 12 desserts made up from 6 ice creams and 6 chocolates.

Combination Principle

Definition of Combination Principle

·         A combination of both Addition Principle and Multiplication Principle?

Solved Example on Multiplication Principle

Ali wants to have his lunch in a food court. He wants to have only 1 or 2 meals from the vast variety of dishes served in the food court. He can choose from 5 Chinese cuisines, 6 Malay cuisines, and 8 types of desserts. So what choices does he have?

If he only wishes to have 1 meal, he can choose from 5 (Chinese cuisines) + 6 ( Malay cuisine) + 8 (desserts) =  19 choices.

If he wishes to have 2 meals of different cuisine, he can choose from 19 X 18 = 342 combinations of meals.
So, if he wishes to have only 1 or 2 meals from the food court, there is 342 + 19 = 361 ways he can have his lunch in the food court.

Permutation

Definition: A way, esp. one of several possible variations, in which a set or number of things can be ordered or arranged especially in linear order.

Formula: _n P _r = n! / (n-r)! 

Problem Solving

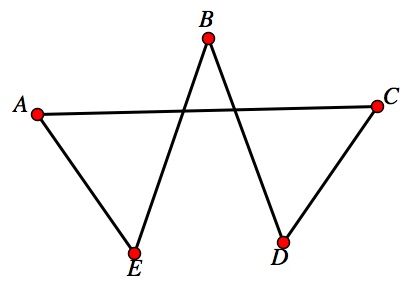
When A,B,C, D and E are lined up for photo shooting sessions, but there’s only 3 persons are allowed. How many different positions can they create for the session?

The answer is 5 X 4 X 3 which is 60 ways.

Or

120 (5!)  / 2 (2!) = 60.
Which means we can choose 5 person from the start. Then we select another one from the leftover 4. At last we select the last person from the leftover 3.

Combination

Definition: A way of selecting several things out of a larger group, where (unlike permutations) order does not matter.

Formula: _nC_r = _nP_r / r! (n-r)! 

Problem Solving

When A,B,C, D and E are lined up for photo shooting sessions, but there’s only 3 persons are allowed. But then the position doesn’t matters.

The answer is 60 (_nP_r    ) / 3! (r!) X 2! (n-r)! = 5.

task 6

QUESTION 1: (DEFINITION)

EULER PATH

An Euler path is a path that uses every edge of a graph 

exactly once

An Eulerian trail (or Eulerian path) is a trail in a graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycleis an Eulerian trail which starts and ends on the same vertex. 

Euler proved that a necessary condition for the existence of Eulerian circuits is that all vertices in the graph have an even degree, and stated without proof that connected graphs with all vertices of even degree have an Eulerian circuit.


EULER CIRCUIT

An Euler circuit is a circuit that uses every edge of a graph 

exactly once.

Every vertex of this graph has an even degree, therefore this is an Eulerian graph.

 Following the edges in alphabetical order gives an Eulerian circuit/cycle.

QUESTION 2.
HOW TO DIFFERENTIATE BETWEEN EULER PATH AND EULER CIRCUIT?

ANSWER:

Euler Path	Euler Circuit
A path that uses every edges of a graph exactly once	A circuit that uses every edges of a graph exactly once
Start and end at different vertices	Start and end at same vertex
If a graph has Euler path, then it must have exactly 2 odd vertices	If a graph has Euler circuit, then all of its vertices must be even vertices

HAMILTON PATH

In the mathematical field of graph theory, a Hamiltonian path (or traceable path) is a path in an undirected graph that visits each vertex exactly once. A Hamiltonian Path can start from one point and ends up at another point.




 HAMILTON CYCLE

A Hamiltonian cycle (or Hamiltonian circuit) is a Hamiltonian path that is a cycle. Hamiltonian Cycle starts from one point and returns to the starting point after traveling it's path.














QUESTION 5
HOW TO DIFFERENTIATE BETWEEN HAMILTON PATH AND HAMILTON CIRCUIT?

ANSWER:

Hamilton Path	Hamilton Circuit
A path that passed every vertex exactly once	A simple circuit that passed every vertex and return to the starting vertex
There is a vertex that has one degree	There is a 2 or more than one degree in the vertex

TASK 4

PRINCIPLE OF MATHEMATICAL INDUCTION:

To prove that P(n) is true for all positive integers n, where P(n) is a propositional function by 2 steps:

Basis      : We show that P(1) is true to show that an initial value/lowest value of n is true for all Z+ of the propositional function.

Inductive : We show that the statement P(n+1) is true for all Z+ of n if P (n) is true.

Similarly, we can say that mathematical induction is a method for proving a property defined that the property for integer n is true for all values of n that are greater than or equal to some initial integer.

                   P (1) ^∀k (P (k) → P (k+1))) → ∀ n P (n)

METHOD OF PROOF:

The proofs of the basis and inductive steps shown in the example illustrate 2 different ways to show an equation is true

-         -- Transforming LHS and RHS independently until they seem to be equal.

-         - Transforming one side of equation until it is seen to be the same as the other side of the equation.

What is the inductive hypothesis  in a proof (ordinary) mathematical induction ?

The simplest and most common form of mathematical induction proves that a statement involving a natural number n holds for all values of n. The proof consists of two steps:

1.    The basis (base case): showing that the statement holds when n is equal to the lowest value that n is given in the question. Usually, n = 0 or n = 1.

2.    The inductive step: showing that, with respect to each n for which the statement holds, then the statement must also hold when n + 1 is substituted for n.

The assumption in the inductive step that the statement holds for some n is called the induction hypothesis (or inductive hypothesis). To perform the inductive step, one assumes the induction hypothesis and then uses this assumption to prove the statement for n + 1.

The choice between n = 0 and n = 1 in the base case is specific to the context of the proof: If 0 is considered a natural number, as is common in the fields of combinatory and mathematical logic, then n = 0. If, on the other hand, 1 is taken as the first natural number, then the base case is given by n = 1.

This method works by first proving the statement is true for a starting value, and then proving that the process used to go from one value to the next is valid. If these are both proven, then any value can be obtained by performing the process repeatedly. It may be helpful to think of the domino effect; if one is presented with a long row of dominoes standing on end, one can be sure that:

1.    The first domino will fall

2.    Whenever a domino falls, its next neighbor will also fall,

So it is concluded that all of the dominoes will fall, and that this fact is inevitable.

EXAMPLE

QUESTION 1.PROVING A FORMULA:
This time we will use arithmetic progression as our example.
a_n = a + (n – 1)d

where d = common difference, in this case we put d = 3
           a= first term of progression, in this case we put a = 5
           n = number of terms
           and n>0.

To form basis step, we prove that P (1) is true.
for a_n = a + (n – 1)d
a₁ = a + (1 – 1)d
a₁ = 5 + ( 0 ) 3 
    = 5 m
Now, for inductive step we need to prove that a_n+1 = a + (n+1 – 1)d.
And thus,
a₂ = a + (1 + 1 – 1) 3
    = 8
and
a₃ = a + (2 + 1 – 1) 3
     = 11
Since we proved that the basis step, P(1) and the inductive step P (n+1) is true we can conclude that the formula is true for n>0.

QUESTION 2.

PROVING A DIVISIBILITY PROPERTY:

Using mathematical induction, prove that for any value of n≥1, 9^{n _} 4ⁿ  is divisible by 5.

Solution:

Let P (n) = 9^{n _} 4ⁿ is divisible by 5, for value of n≥1.

Basis      : Proof that P (1) is valid for the statement

P (1) = 9^{n _} 4ⁿ 

    = 9 - 4

    = 5 (which is divisible by 5)

Hence, the statement is true.

Inductive: We proof that if P (n) is true, then P (n+1) is true for integer k≥1,

Inductive Hypothesis

P (n) = 9^{n _} 4ⁿ   / 5 = m

         = 9^{n _} 4ⁿ = 5 m
(In this case m is an integer)

P (n+1) = 9 ⁿ⁺¹ -   4 ⁿ⁺¹ 

                = 9. 9ⁿ - 4. 4ⁿ 

                = 5. 9ⁿ + 4. 9ⁿ  - 4.4ⁿ

                        = 5. 9ⁿ + 4 ( 9^{n _} 4ⁿ  )

                = 5. 9ⁿ + 4 (5 m)

                = 5. 9ⁿ + 5 (4 m)

                = 5 ( 9ⁿ + 4m)
So, since ( 9ⁿ + 4m) is an integer valid for n and m is an integer we can conclude that the statement is true by proving P (n) = 1 is true and P (n+1) is also true.

QUESTION 3.
PROVING INEQUALITIES Mathematical induction can be used to prove a variety of inequalities that hold for all positive integers greater than a particular positive integer.

Example: Prove 5n+5 <= n² for all positive integers n>=6.

                Proof = Let P(n) be the statement  5n+5 <=n²

                Basis step : n=6, Since 5n+5= 5(6)+5 <= 6² = n² , 35 <= 36

            Inductive step : Assume P(n) : 5n+5<= n², for some integer n>=6. 

Use the induction hypothesis to prove 5(n+1) +5 <=(n+1)².

                First rewrite 5(n+1)+5 so that it uses 5n+5 =

                5(n+1)+5=(5n+5)+5

   By induction hypothesis we know:

                (5n+5)+5 <=n²+5

   Now we need to show

                n²+5 <=(n+1)²= n² +2n + 1

    to see this we note that when n>=2,

                2n+1 >= 2(2)+1 = 5

    (and so this is also valid for n >=6)

Thus, when n>=6,

                5(n+1)+5 = (5n+5)+5

                (5n+5)+5 <= n²+5

                n²+5 <= n²+2n+1

                n² +2n +1 =(n+1)²

which shows 5(n+1) +5 <= (n+1)² . By the principal of mathematical induction it follows that 5n+5<=n² for all integers n >=6 .